SPSS macro for Box-Cox transformations

In statistics, the Box-Cox transformation of the response variable Y is used to make the linear model more appropriate to the data. It can be used to attempt to impose linearity, reduce skewness or stabilize the residual variance. The Box-Cox transformation is defined as:

However, the Box-Cox transformation is not yet supported in SPSS. I write a macro to compute log-likelihood for different lambda. If you have any better way, please let me know.

*
*Box-Cox transformation
*

SET MXLOOP =9999.
MATRIX.
GET X/VARIABLES=x1,x2/MISSING=OMIT.
GET Y/VARIABLE=y /MISSING=OMIT.
COMPUTE NR =NROW(X).
COMPUTE NC =NCOL(X).
COMPUTE XX=MAKE(NR,NC+1,1).
COMPUTE YYG=MAKE(NR+1,1,1).
LOOP I=1 TO NR.
COMPUTE XX(I,1)=1.
COMPUTE YYG(I+1)=Y(I)*YYG(I).
LOOP J=2 TO NC+1.
COMPUTE XX(I,J)=X(I,J-1).
END LOOP.
END LOOP.
COMPUTE YG=YYG(NR+1).
COMPUTE BOXCOX=MAKE(61,2,0).
LOOP TEMP=1 TO 61.
COMPUTE LAMBDA=-3.1 + TEMP * 0.1.
DO IF LAMBDA=0.
COMPUTE YLAM=LN(Y).
ELSE.
COMPUTE YLAM=(Y&**LAMBDA-1)/LAMBDA.
END IF.
COMPUTE BETA=INV(T(XX)*XX)*T(XX)*YLAM.
COMPUTE SSE = T(YLAM-XX*BETA)*(YLAM-XX*BETA).
COMPUTE LOGLIKE=-1*NR/2*LN(SSE)-NR/2+(LAMBDA-1)*LN(YG).
COMPUTE BOXCOX(TEMP,1)= LAMBDA.
COMPUTE BOXCOX(TEMP,2)= LOGLIKE.
END LOOP.
SAVE BOXCOX /OUTFILE=*.
END MATRIX.
RENAME VARIABLES COL1= LAMBDA COL2= LOGLIKE.
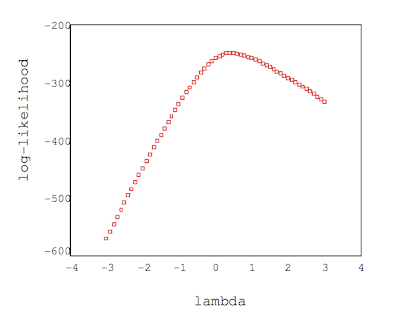
GRAPH
/SCATTERPLOT(BIVAR)=LAMBDA WITH LOGLIKE /MISSING=LISTWISE
/TITLE= 'Log-Likelihood versus lambda'.

How to..

Step 1. Open your sav file

Step 2. File-→New-→Syntax

Step 3. Copy the syntax into syntax window

Step 4. From the SPSS Syntax editor menu → Run→All